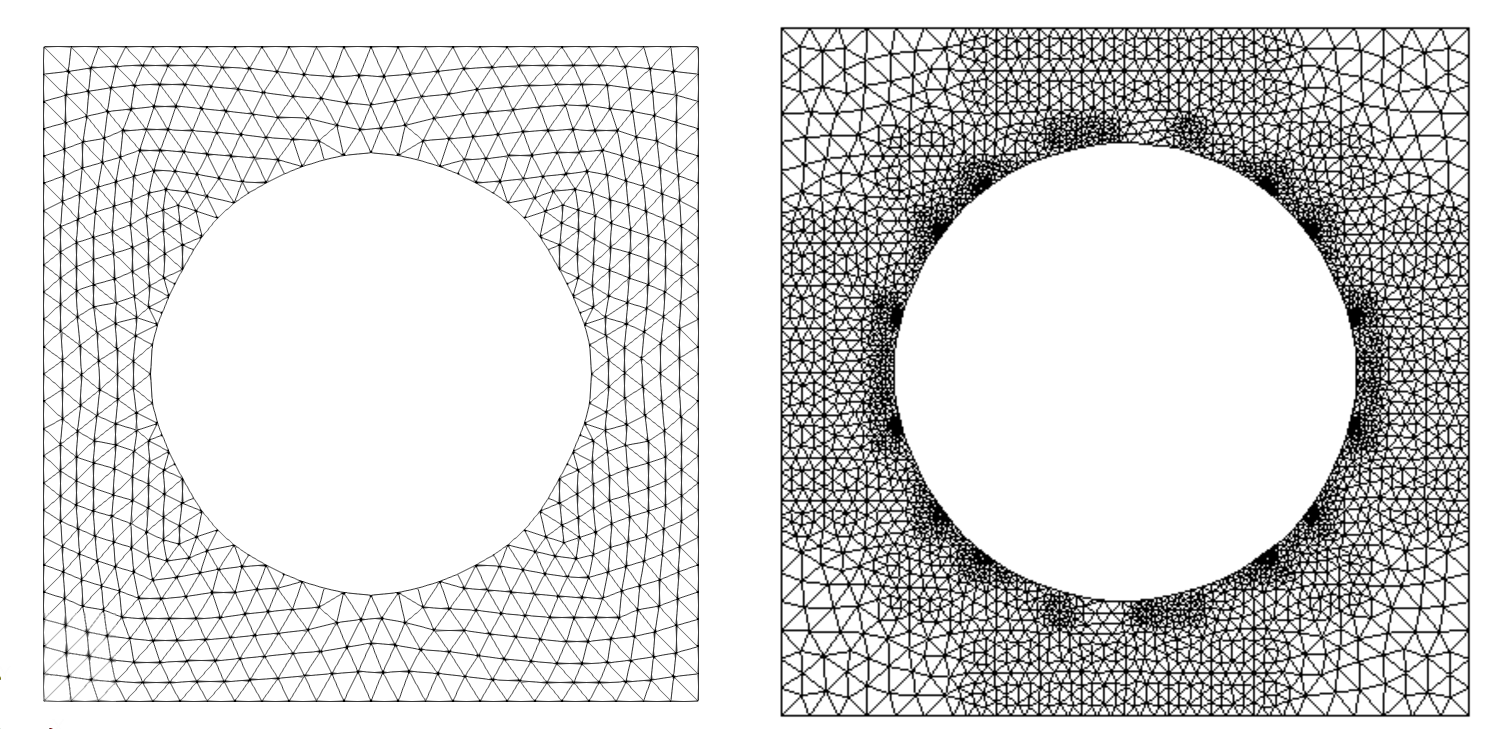
Finite Element Analysis (FEA) is a numerical method that stitches up local solutions into global ones with the aid of meshes. The accuracy of the solution obtained is directly dependent on the refinement of the mesh used. Erroneous regions of the underlying FE domain can be captured by error functions or point clouds, which can further be used to adaptively refine meshes and improve the solution accuracy.

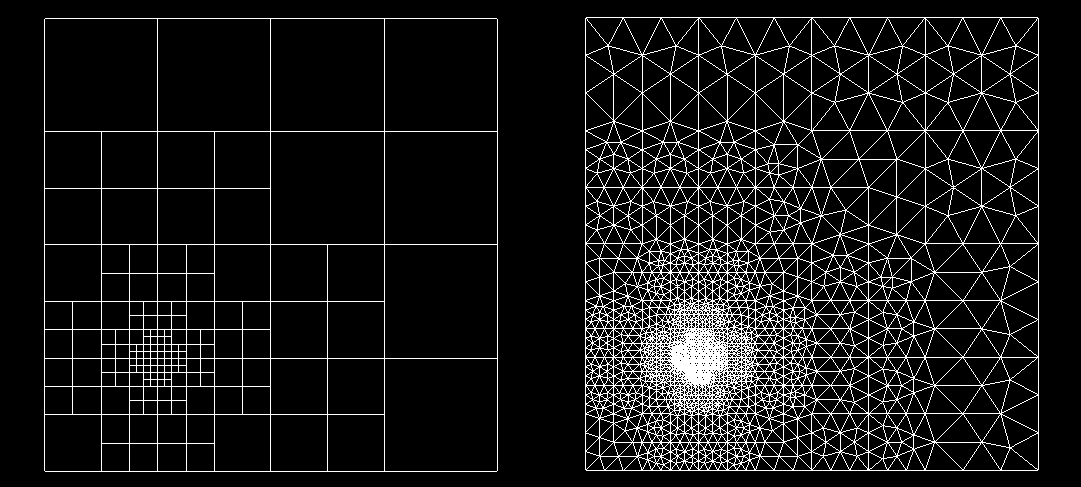
This work implements mesh generation algorithms introduced by Bern, Eppstein and Gilbert, in the paper - Provably Good Mesh Generation. It takes in a user-defined error function or point cloud which quantifies the underlying error, based on which a preliminary quadtree is constructed. Methods of balancing and strong balancing as prescribed by Bern and Eppstein are applied after which stencils are fit, to obtain the final adaptively refined mesh. The implementation was successfully used to demonstrate the reduction of error by solving an obstacle problem. This work was conducted under the guidance of Prof. Ramsharan Rangarajan at the Mechanics and Computation Lab, Department of Mechanical Engineering, Indian Institute of Science.

Some highlights of this work are -

  • This work was used to generate adaptively refined meshes for user-defined error functions and point clouds, with provable guarantees of being good quality triangulations.
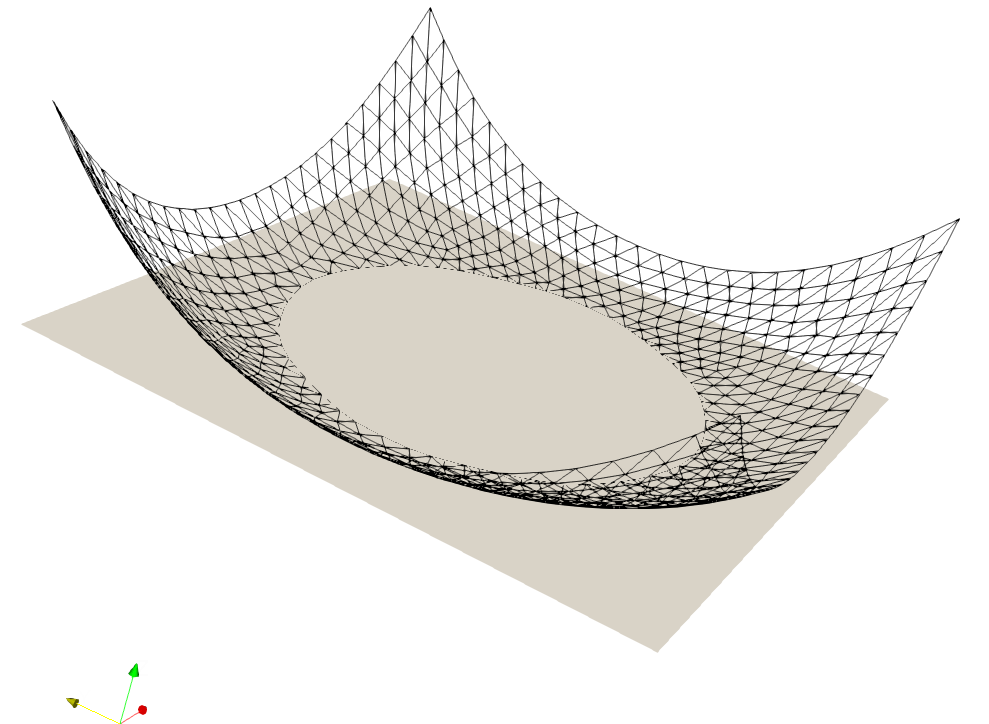
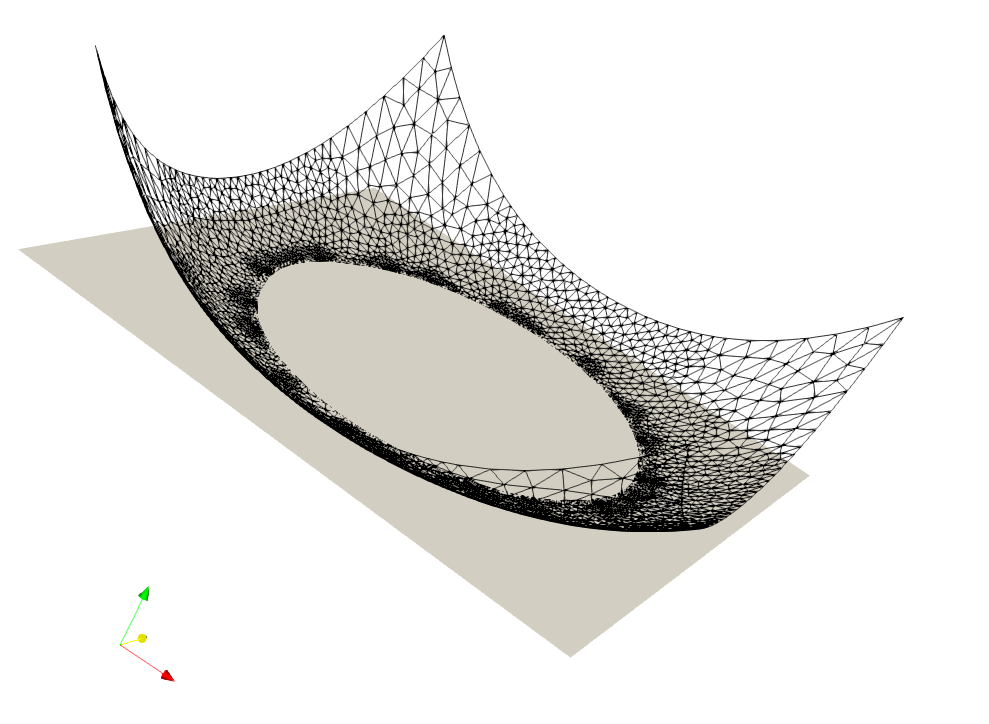
  • The efficacy of this work was demonstrated by solving an obstacle problem with a regular mesh and an adaptively refined one, followed by a comparison of solution accuracies.
  • The code for this work can be found here.

Examples & Results

Preliminary quadtree for error function: f(x , y) = k + xy , k = 0.1

Strongly balanced quadtree

Quadtree for error function: f(x , y) = k + xy , k = 0.01

Adaptively refined mesh obtained

Obstacle Problem: Regular mesh used to study contact between the clamped membrane and flat plate (obstacle)

Adaptively refined mesh generated to improve the solution accuracy of the problem

Displacement Flux v/s Theta (contact region boundary). True solution value of flux = 0. Obtained flux range = [-0.1, 0.1]

Displacement Flux v/s Theta (contact region boundary). True solution value of flux = 0. Obtained flux range = [-0.03, 0.03]

Obstacle Problem

The obstacle problem studies the contact region boundary between a thin square membrane clamped at its four corners and a flat infinite plate which acts as an obstacle. Two meshes were tested, a regular triangulation and an adaptively refined triangulation based on an input point cloud. The solution obtained by the adaptively refined mesh was in the range [-0.03, 0.03] as opposed to the range [-0.1, 0.1] obtained by the regular mesh. This demonstrates nearly an order of magnitude higher accuracy in the adaptively refined mesh, since the true solution for the displacement flux = 0.

View initial guesses perturbed to final positions: Regular Mesh & Adaptive Mesh

Stencil Fitting

Bern and Eppstein recommend the fitting of stencils to obtain provably good meshes after generating the strongly balanced quadtree, the animation for which can be viewed here.

Adaptively Refined Meshes From Point Clouds

A hole in a plate can be analysed as shown using an adaptively refined mesh. The inputs include the dimensions of the plate and a point cloud describing the hole. Click here to view the animation.

Any arbitrary point cloud (like the flower shown in the image) can be used to generate a mesh which can be refined in an adaptive manner, using this algorithm. Click here to view the animation.